直线绘制
- 逐点比较法
- 正负法
- 数值微分算法 DDA
- bresenham算法
- 改bresenham
起始点\(P_0(x_0, y_0)\) 终点\(P_1(x_1, y_1)\)
逐点比较法
https://blog.csdn.net/ABC13222880223/article/details/83176512
正负法
https://blog.csdn.net/qq_26982531/article/details/69946738
数值微分算法 DDA
- 计算其斜率
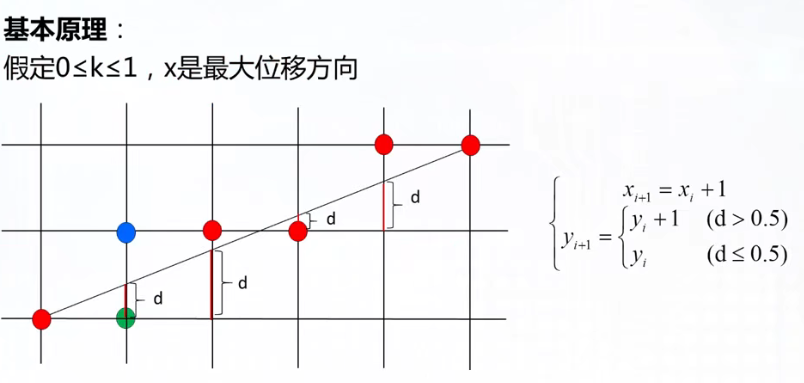
步进的形式,已知 $P_i$ 那么其下一个点就可以算出
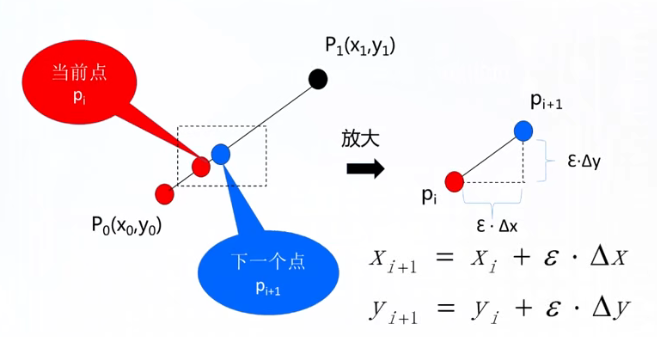
因为像素是离散的,在斜率不同的情况下,渐进的步长是不一样的!
- 斜率小于1的时候以x轴的方向递进
- 斜率大于1的时候以y轴的方向递进
基本的代码如下!
void LineDDA(Point begin, Point end)
{
int dx = end.x - begin.x;
int dy = end.y - begin.y;
int steps,k;
float xIncrement, yIncrement;
float x = begin.x;
float y = begin.y;
// 最大位移方向的判定
if (fabs(dx) > fabs(dy))
{
steps = fabs(dx);
}
else
{
steps = fabs(dy);
}
// x,y方向上的增量
xIncrement = float(dx) / float(steps);
yIncrement = float(dy) / float(steps);
setPixel(round(x), round(y));
for (k=0; k < steps; k++)
{
x += xIncrement;
y += yIncrement;
setPixel(round(x), round(y));
}
}
优:简单直观,容易实现 缺:有浮点数和浮点运算,效率不高
bresenham算法
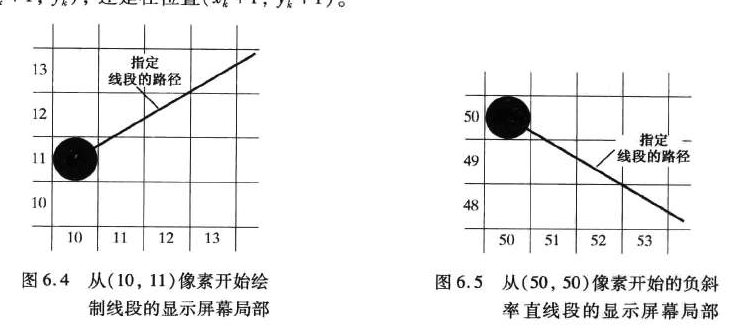
先假设斜率为 $0\le k \le 1$ 在当前点 $p_i$ 的候选点就有如图6.4的数据,$(10, 11) $的下一个点应该是考虑 $(10+1, 11)$ 和 $ (10+1, 11+1)$ 两个点。 假设第k个点 $P_k(x_k, y_k)$,而其公式是 \(y=kx+b \tag{1}\) 那么点 $P_k$的两个候选点分别是 $(x_k+1, y_k)$ 和 $(x_k+1, y_k+1)$,计算这两个候选点与直线上的点的差距; 设直线的方程式是:(m是斜率) \(\begin{align} \begin{split} \because y&=mx+b \Rightarrow y_{k+1}=m(x_k+1)+b \\ d_{lower}&=y_{k+1}-y_k \\ d_{upper}&=(y_k+1)-y_{k+1} \\ \therefore d_{lower}&=m(x_k+1)+b - y_k \\ d_{upper}&=y_k+1-m(x_k+1)-b \end{split} \tag{2} \end{align}\) 两个像素到直线的距离差就是 \(d_{lower}-d_{upper} = 2m(x_k+1)-2y_k+2b-1 \tag{3}\)
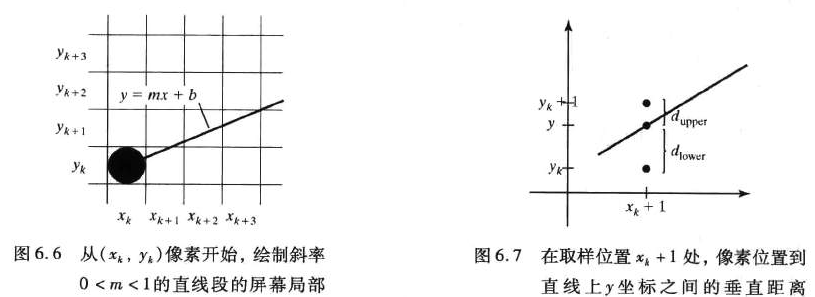
两个候选点的选择就看 $d_{lower}-d_{upper}$的符号了,如果是正,那么就选择 $d_{upper}$ 否则 $d_{lower}$ 设 $\Delta y$ 和 $\Delta x$ 分别为两端点的垂直和水平偏移量,令 $ m = \Delta{y} / \Delta{x}$ ;
\[\begin{align} \begin{split} \Rho_k &= \Delta{x}(d_{lower}-d_{upper}) \\ &=2\Delta{y}\cdot x_k-2\Delta{x}\cdot y_k + \underbrace{( 2\Delta{y} + \Delta{x}(2b - 1))}_C \end{split} \tag{4} \end{align}\]$\Delta{x}>0$,所以 $\Rho_k $的符号与 $d_{lower}-d_{upper}$相同参数 $c$ 是一个常量,它和像素位置无关。
\[\begin{align} \begin{split} \Rho_{k+1} &=2\Delta{y}\cdot x_{k+1}-2\Delta{x}\cdot y_{k+1} + C \\ \Rho_{k+1} - \Rho_k &= 2\Delta{y}\cdot (x_{k+1} - x_k) - 2\Delta{x}\cdot (y_{k+1} - y_k) \\ \because |斜率m| < 1 \Rightarrow x_{k+1} &= x_k+1 \\ \therefore \Rho_{k+1} &= \Rho_k + 2\Delta{y} - 2\Delta{x}(y_{k+1} - y_k) \\ \end{split} \tag{5} \end{align}\]取 $(x_0, y_0)$,转换计算就有 $\Rho_0 =2\Delta{y} - \Delta{x}$

// |m| < 1
void LineBresnhan(Point begin, Point end)
{
// 计算delta_x delta_y
int dx = fabs(end.x - begin.x), dy = fabs(end.y - begin.y);
// 计算P0的符号
int p = 2 * dy - dx;
int twoDy = 2 * dy, twoDyMinusDx = 2 * (dy - dx);
int x, y;
// 保持从左到右,x的增量恒为正
if (begin.x > end.x)
{
x = end.x;
y = end.y;
end.x = begin.x;
}
else
{
x = begin.x;
y = begin.y;
}
setPixel(begin.x, begin.y);
while(x < end.x)
{
x++;
if(p < 0)
p += twoDy;
else
{
y++;
p += twoDyMinusDx;
}
setPixel(x, y);
}
}
改bresenham