开根号有两种比较常见的方式:牛顿迭代法和二分法。
二分法
public static double SqrtBinary(double value)
{
/**二分法实现开方
需要注意的是:
1.初始上界是A+0.25,而不是A
2.double型的精度DBL_EPSILON,不能随意指定
*/
double a = 0.0, b = value + 0.25, m; // b = A 是错误的上届
// while(b - a > 2*DBL_EPSILON){ //sometimes dead cycle when m == a or m == b.
for (;;)
{
m = (b + a) / 2;
if (m - a < DBL_EPSILON || b - m < DBL_EPSILON) break;
if ((m * m - value) * (a * a - value) < 0) b = m;
else a = m;
}
return m;
}
牛顿迭代法
public static double SqrtND(double value)
{
double x0 = value + 0.25, x1, xx = x0;
for (;;)
{
x1 = (x0 * x0 + value) / (2 * x0);
if (Math.Abs(x1 - x0) <= DBL_EPSILON) break;
if (xx == x1) break; //to break two value cycle.
xx = x0;
x0 = x1;
}
return x1;
}
因为本人是用unity的开发者,简单写一下测试的demo代码,看看在android上的性能表现
具体的代码在github
结合unity的Mathf.sqrt和System.Math.sqrt来测试
测试结果
- 在使用mono打包的情况下
SqrtBinary 耗时=> 2486800 SqrtND 耗时=> 1400908 Mathf.Sqrt 耗时=> 222906 Math.Sqrt 耗时=> 192895 ======================= SqrtBinary 耗时=> 2574513 SqrtND 耗时=> 1401643 Mathf.Sqrt 耗时=> 212643 Math.Sqrt 耗时=> 182390 ======================= SqrtBinary 耗时=> 2504743 SqrtND 耗时=> 1395411 Mathf.Sqrt 耗时=> 213225 Math.Sqrt 耗时=> 181148 =======================在每轮20W次的情况下,执行三轮,发现
Math.Sqrt > Mathf.Sqrt > SqrtND > SqrtBinary,C#的math是最高效的,查看Mathf.sqrt后,可以看到unity的mathf对数据进行了多次类型转换,故mathf的消耗比math要打属正常。 - 在使用il2cpp打包的情况下
SqrtBinary 耗时=> 1744842 SqrtND 耗时=> 430589 Mathf.Sqrt 耗时=> 27215 Math.Sqrt 耗时=> 49882 ======================= SqrtBinary 耗时=> 1770444 SqrtND 耗时=> 433782 Mathf.Sqrt 耗时=> 26203 Math.Sqrt 耗时=> 49729 ======================= SqrtBinary 耗时=> 1693556 SqrtND 耗时=> 429176 Mathf.Sqrt 耗时=> 26054 Math.Sqrt 耗时=> 50526 =======================在每轮20W次的情况下,执行三轮,发现
Mathf.Sqrt > Math.Sqrt > SqrtND > SqrtBinary,居然是unity的mathf最高效,看来是unity的il2cpp做了什么不得了的事情了,后面我们在去看看原因。
原因:
通过查看il2cpp生成的cpp文件
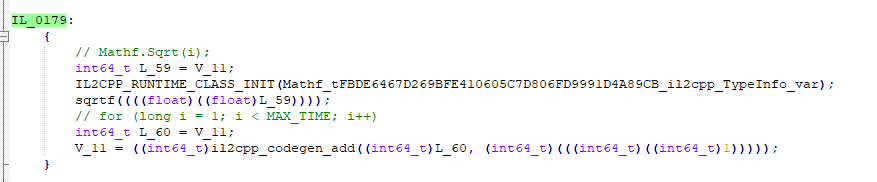
我们可以看到,两个方法在生成上的差异就仅仅只是精度的差异!所以效率在于精度
空间换时间
static int[] table = { 0, 16, 22, 27, 32, 35, 39, 42, 45, 48, 50, 53, 55, 57, 59, 61, 64, 65, 67, 69, 71, 73, 75, 76, 78, 80, 81, 83, 84, 86, 87, 89, 90, 91, 93, 94, 96, 97, 98, 99, 101, 102, 103, 104, 106, 107, 108, 109, 110, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 128, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 144, 145, 146, 147, 148, 149, 150, 150, 151, 152, 153, 154, 155, 155, 156, 157, 158, 159, 160, 160, 161, 162, 163, 163, 164, 165, 166, 167, 167, 168, 169, 170, 170, 171, 172, 173, 173, 174, 175, 176, 176, 177, 178, 178, 179, 180, 181, 181, 182, 183, 183, 184, 185, 185, 186, 187, 187, 188, 189, 189, 190, 191, 192, 192, 193, 193, 194, 195, 195, 196, 197, 197, 198, 199, 199, 200, 201, 201, 202, 203, 203, 204, 204, 205, 206, 206, 207, 208, 208, 209, 209, 210, 211, 211, 212, 212, 213, 214, 214, 215, 215, 216, 217, 217, 218, 218, 219, 219, 220, 221, 221, 222, 222, 223, 224, 224, 225, 225, 226, 226, 227, 227, 228, 229, 229, 230, 230, 231, 231, 232, 232, 233, 234, 234, 235, 235, 236, 236, 237, 237, 238, 238, 239, 240, 240, 241, 241, 242, 242, 243, 243, 244, 244, 245, 245, 246, 246, 247, 247, 248, 248, 249, 249, 250, 250, 251, 251, 252, 252, 253, 253, 254, 254, 255 }; /** * A faster replacement for (int)(java.lang.Math.sqrt(x)). Completely * accurate for x < 2147483648 (i.e. 2^31)... */ static long SSqrt(long x) { long xn; if (x >= 0x10000) { if (x >= 0x1000000) { if (x >= 0x10000000) { if (x >= 0x40000000) { xn = table[x >> 24] << 8; } else { xn = table[x >> 22] << 7; } } else { if (x >= 0x4000000) { xn = table[x >> 20] << 6; } else { xn = table[x >> 18] << 5; } } xn = (xn + 1 + (x / xn)) >> 1; xn = (xn + 1 + (x / xn)) >> 1; return ((xn * xn) > x) ? --xn : xn; } else { if (x >= 0x100000) { if (x >= 0x400000) { xn = table[x >> 16] << 4; } else { xn = table[x >> 14] << 3; } } else { if (x >= 0x40000) { xn = table[x >> 12] << 2; } else { xn = table[x >> 10] << 1; } } xn = (xn + 1 + (x / xn)) >> 1; return ((xn * xn) > x) ? --xn : xn; } } else { if (x >= 0x100) { if (x >= 0x1000) { if (x >= 0x4000) { xn = (table[x >> 8]) + 1; } else { xn = (table[x >> 6] >> 1) + 1; } } else { if (x >= 0x400) { xn = (table[x >> 4] >> 2) + 1; } else { xn = (table[x >> 2] >> 3) + 1; } } return ((xn * xn) > x) ? --xn : xn; } else { if (x >= 0) { return table[x] >> 4; } } } return -1; }目前测试来看,在il2cpp的情况下还是Mathf.sqrt比较高效!
倒数速算法
先上wikipedia link给大佬们看看