纲要
- 回顾
- 推导
回顾
先说明一下勾股定理
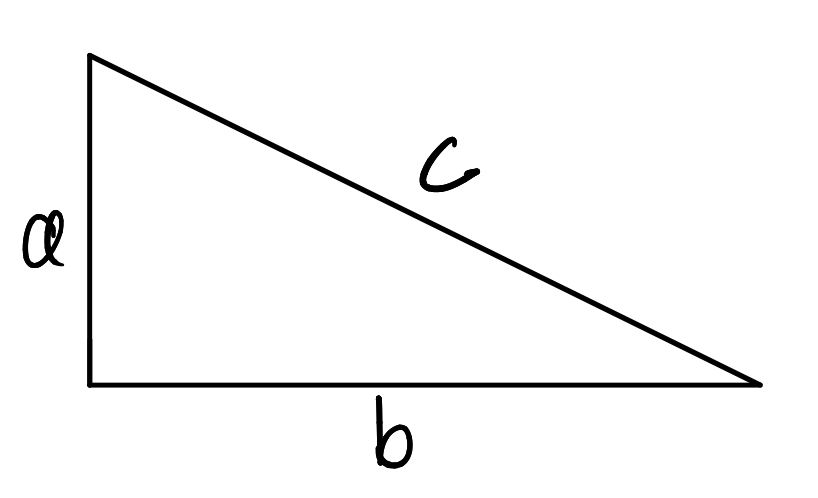
有理数又是个什么概念呢?
可以表达为两个整数比的数($\frac{a}{b}$, $b\neq 0$)被定义为有理数
推导
基于上述的公式,假设$a=b=1$,那么$c$大约是在$1\lt c \lt 1.5$
由:
$c^2=a^2+b^2$及$a=b=1$
得:
$2 = c^2$
先假设$c = \frac{z}{m}$, 就是先假设$c$是个有理数,分子为整数$z$, 分母为整数$m$, 且$z$和$m$互质,就是说他们是不能再化简的,比如$\frac{2}{6}$还能化简为$\frac{1}{3}$, 所以$z$和$m$不能同时为偶数
再得:
$2 = \frac{z^2}{m^2}$
进行变换后: $2*m^2=z^2$
所以$z^2$为偶数,由于偶数的平方还是偶数,奇数的平方还是奇数,(奇数可表示为2n+1, 则 $(2n+1)^2 = 4n*n+4n+1$, 仍然是个奇数)
所以$z$是偶数,$z$表示为$2*n$
推得
$m^2 = 2*n^2$
则$m$为偶数
得到推论$z$和$m$同时为偶数,这和假设$z$和$m$互质矛盾,所以:
两个短边为1的等腰直角三角形的最长边不是个有理数分式!